D2L-53-循环神经网络RNN

Last updated Apr 1, 2022 Edit Source

• All
• Rnn
• Deep learning
• Neural network

Tags: #RNN #DeepLearning #NeuralNetwork

• 基于马尔可夫假设的N元语法（n-gram）需要存储大量的参数。在 $n$ 逐渐增大的过程中，n-gram模型的参数大小 $|W|$ 与序列长度 $n$ 是指数关系：$$|W|=|\mathcal{V}|^n $$ ($|\mathcal{V}|$ 是单词的数目)
• 因此, 我们将目光转向了 隐变量自回归模型. 隐状态 $h_{t-1}$ 能够(近似地)存储当前时间步之前所有输入的综合影响: $$P\left(x_{t} \mid x_{t-1}, \ldots, x_{1}\right) \approx P\left(x_{t} \mid h_{t-1}\right)$$
  • 进而, 我们可以使用当前的输入和上一个隐状态来生成当前的隐状态: $$h_{t}=f\left(x_{t}, h_{t-1}\right)$$ 只要函数 $f$ 足够强大, 就能将所有信息都综合到 $h_t$ 里面, 不丢失任何信息. 当然, 这样的开销也是很大的.

• Recurrent neural networks (RNNs)就是带有隐状态的神经网络.

• RNN和 MLP 其实是非常相似的, 它们唯一的区别就是有没有隐状态 $h_{t}$
• MLP $$\begin{aligned} \mathbf{H}&=\phi\left(\mathbf{X} \mathbf{W}{x h}+\mathbf{b}{h}\right)\\ \mathbf{O}&=\mathbf{H} \mathbf{W}{h q}+\mathbf{b}{q}\end{aligned}$$
• RNN $$\begin{aligned} \mathbf{H}t&=\phi\left(\textcolor[RGB]{255, 83, 61}{\mathbf{H}{t-1}\mathbf{W}{h h}}+\mathbf{X} \mathbf{W}{x h}+\mathbf{b}{h}\right)\\ \mathbf{O}&=\mathbf{H} \mathbf{W}{h q}+\mathbf{b}_{q}\end{aligned}$$
• 注意在加上偏置的时候触发了PyTorch的广播机制(Broadcasting, see Section 2.1.3)
• 下面是一些图例:

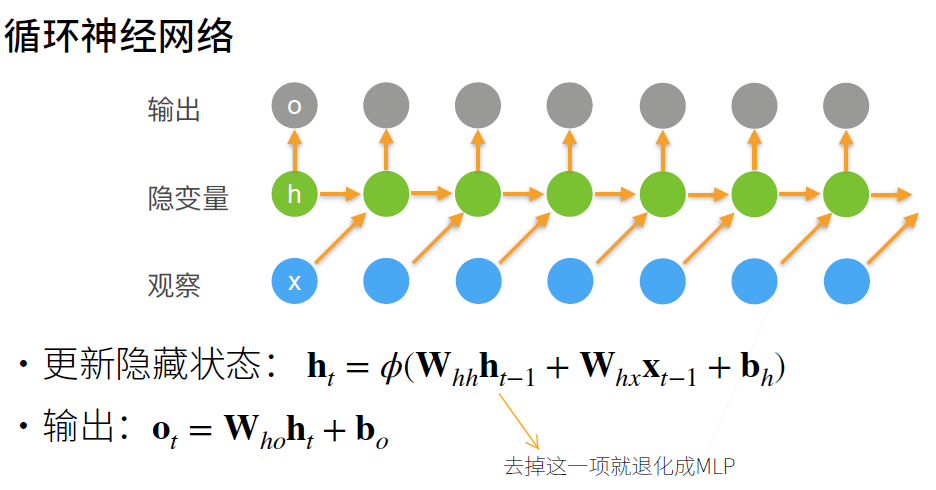
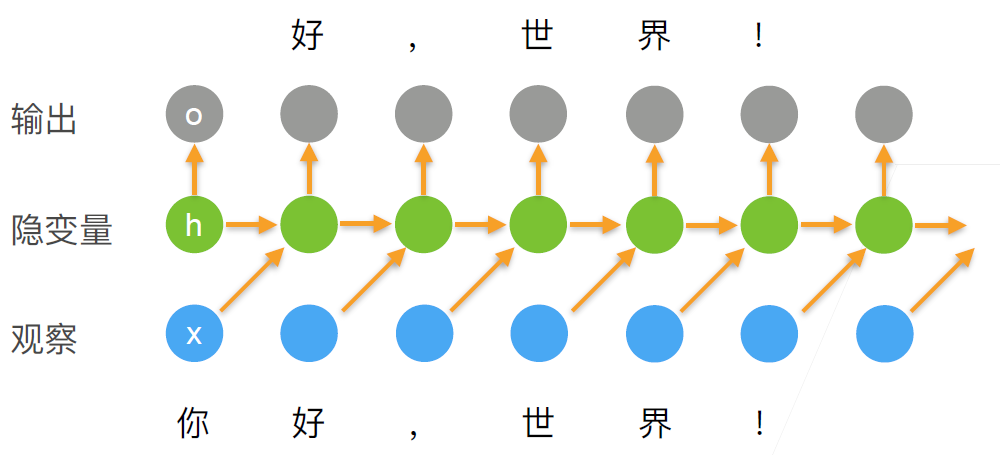
• 值得注意的一点是, 因为我们在每一个时间步都使用的是同一个参数矩阵 $\mathbf{W}_{hh}$, 所以RNN的参数大小并不会随着时间步的增长而增长.

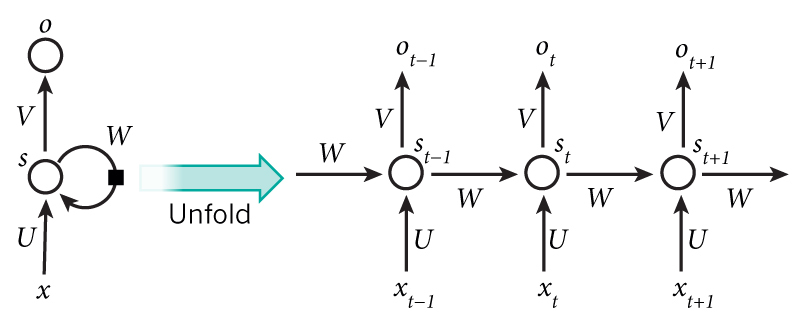
• 尽管每一次计算都需要利用上一次的 $\mathbf H_{t-1}$, 但是使用的参数 $\mathbf{W}_{hh}$ 都是一样的. 也就是说, 每一层的隐状态的计算方式是完全一样的, 这一次的输出就是下一次的输入, 是一个递归的关系, 这也是Recurrent的含义.

  • 递归计算隐状态的层自然就叫做"递归层(recurrent layer)"

• 公式里面是:

• 实际上可以简化成:

• RNN的计算可以表示为: ^ba5f9a

• 因为RNN的递归层存在环路, 所以RNN不属于前馈神经网络(Feedforward neural network).

• Review: Cross_Entropy-交叉熵

• 虽然我们可以使用整个句子的概率 $P\left(x_{1}, \ldots, x_{T}\right)$ 来评价模型的质量, 但由于短序列的概率很可能比长序列大许多, 我们很难直观的评价模型的好坏.

• 一个自然的想法就是将整个句子的概率"除以"句子的长度, 用"每个字符的概率"作为评价指标. 利用信息论的知识, 我们可以结合交叉熵的概念: 一个好的预测模型应该输出和真实句子尽可能相似的结果. 我们可以用交叉熵来衡量模型的输出概率 $q(x_i)=P\left(x_{i} \mid x_{t-1}, \ldots, x_{1}\right)$ 和真实序列分布 $p(x_i)$ 的差距: $$\begin{aligned} CE(p,q)&=-\sum_i^{|\mathcal{V}|}p(x_i)\log q(x_i)\\ (\text{独热编码})&=-\log q(x_t)\&=-\log P\left(x_{t} \mid x_{t-1}, \ldots, x_{1}\right)\end{aligned}$$

  • 其中 $|\mathcal{V}|$ 是所有可能的 $x_i$ 个数, 因为真实序列是已知的, 相当于独热编码, 所以只剩下 $x_i=x_t$ 的一项, 其中 $x_t$ 是在时间步 $t$ 从该序列中观察到的实际词元

• 将整个序列里面所有位置的交叉熵综合起来, 再取平均得到: $$-\frac{1}{n} \sum_{t=1}^{n} \log P\left(x_{t} \mid x_{t-1}, \ldots, x_{1}\right)$$

• 由于历史原因，自然语言处理的科学家更喜欢使用一个叫做_困惑度_（perplexity）的量。 简而言之，它是上式的指数： $$\exp \left(-\frac{1}{n} \sum_{t=1}^{n} \log P\left(x_{t} \mid x_{t-1}, \ldots, x_{1}\right)\right)$$

困惑度的最好的理解是“下一个词元的实际选择数的 调和平均数(Harmonic mean)”。 我们看看一些案例：

• 在最好的情况下，模型总是完美地估计标签词元的概率为 $1$。 在这种情况下，模型的困惑度为 $1$。
• 在最坏的情况下，模型总是预测标签词元的概率为 $0$。 在这种情况下，困惑度是正无穷大。
• 在基线上，该模型的预测是词表的所有可用词元上的均匀分布。 在这种情况下，困惑度等于词表中唯一词元的数量 $|\mathcal{V}|$。 事实上，如果我们在没有任何压缩的情况下存储序列， 这将是我们能做的最好的编码方式。 因此，这种方式提供了一个重要的上限， 而任何实际模型都必须超越这个上限。¹

RNN中output和hidden_state的区别