D2L-55-在时间上反向传播
# Backpropagation Through Time
Tags: #Backpropagation #RNN
- 和正向传播的时候一样, RNN在反向传播的时候需要在时间步上面进行迭代, 这可能导致梯度问题.
- 下面我们先大概分析在"时间上"反向传播的不同之处, 然后简要介绍一些缓解梯度问题的训练方法, 最后, 我们详细的分析一下在时间上反向传播的细节问题.
- 这篇笔记以 8.7. Backpropagation Through Time — Dive into Deep Learning 为基础.
# 在时间上反向传播/RNN的反向传播
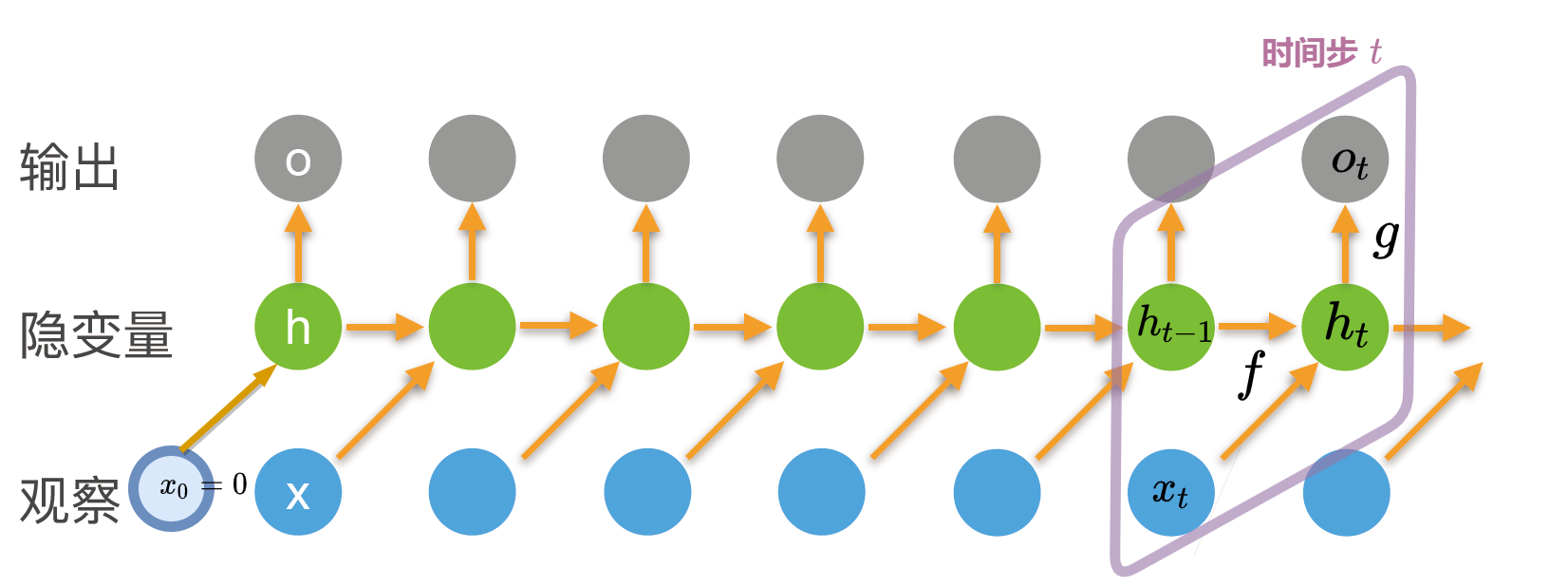
# 模型
- 我们可以把RNN的计算简化为两个函数: $f$ 更新隐状态, $o_t$ 根据隐状态生成输出: $$\begin{aligned}h_t &= f(x_t, h_{t-1}, w_h),\o_t &= g(h_t, w_o),\end{aligned}$$
- 其中:
- $x_t$ 是 $t$ 时刻的输入, 注意下标是时间步而不是在序列里的位置
- $h_t$ 是 $t$ 时刻的隐状态
- $w_h$ 是隐藏层的权重
- $w_o$ 是输出层的权重
# 损失函数
- 损失函数里面, 我们将 $x_1, \ldots, x_T$ 输入模型, 得到输出 $o_1, \ldots, o_T$, 将 $y_1, \ldots, y_T$ 与每一个输出进行比较, 再取平均. 其中 $w_h, w_o$ 是我们需要优化的目标. $$L(x_1, \ldots, x_T, y_1, \ldots, y_T, w_h, w_o) = \frac{1}{T}\sum_{t=1}^T l(y_t, o_t)$$
# 求梯度: $\frac{\partial L}{\partial w_o}$
- 对于 $w_o$ 的梯度很好计算, 因为每一个输出仅依赖于当前时刻的隐状态 $h_t$, 不存在递归关系. $$\begin{aligned}\frac{\partial L}{\partial w_o}& = \frac{1}{T}\sum_{t=1}^T \frac{\partial l(y_t, o_t)}{\partial w_o}\&= \frac{1}{T}\sum_{t=1}^T \frac{\partial l(y_t, o_t)}{\partial o_t} \frac{\partial g(h_t, w_o)}{\partial w_o}\end{aligned}$$
# 求梯度: $\frac{\partial L}{\partial w_h}$
在下面的式子里面, 前两个因子都很好计算, 而递归关系隐藏在 ${\partial h_t}/{\partial w_h}$ 里面. $$\begin{aligned}\frac{\partial L}{\partial w_h}& = \frac{1}{T}\sum_{t=1}^T \frac{\partial l(y_t, o_t)}{\partial w_h}\&= \frac{1}{T}\sum_{t=1}^T \frac{\partial l(y_t, o_t)}{\partial o_t} \frac{\partial g(h_t, w_o)}{\partial h_t} \frac{\partial h_t}{\partial w_h}\end{aligned}$$
$h_t = f(x_t, h_{t-1}, w_h)$ 而 $h_{t-1}$ 同样依赖于 $w_h$, 所以根据求导法则有: $$\frac{\partial h_t}{\partial w_h}= \frac{\partial f(x_{t},h_{t-1},w_h)}{\partial w_h} +\frac{\partial f(x_{t},h_{t-1},w_h)}{\partial h_{t-1}} \frac{\partial h_{t-1}}{\partial w_h}$$ 用颜色标识出每部分的求导对象: $$\textcolor{red}{\frac{\partial h_t}{\partial w_h}}= \frac{\partial f(x_{t},h_{t-1},\textcolor{blue}{w_h})}{\textcolor{blue}{\partial w_h}} +\frac{\partial f(x_{t},\textcolor{green}{h_{t-1}},w_h)}{\textcolor{green}{\partial h_{t-1}}} \textcolor{red}{\frac{\partial h_{t-1}}{\partial w_h}}$$ 其中红色的部分构成了递归.
对于递推公式 $a_{t}=b_{t}+c_{t}a_{t-1}$, $a_{0}=0$. 我们可以求出通项公式为1: $$a_{t}=b_{t}+\sum_{i=1}^{t-1}\left(\prod_{j=i+1}^{t}c_{j}\right)b_{i}$$
再进行替换: $$\begin{aligned}a_t &= \textcolor{red}{\frac{\partial h_t}{\partial w_h}},\\ b_t &= \frac{\partial f(x_{t},h_{t-1},\textcolor{blue}{w_h})}{\textcolor{blue}{\partial w_h}}, \\ c_t &= \frac{\partial f(x_{t},\textcolor{green}{h_{t-1}},w_h)}{\textcolor{green}{\partial h_{t-1}}},\end{aligned}$$ 得到: $$\textcolor{red}{\frac{\partial h_t}{\partial w_h}} =\frac{\partial f(x_{t},h_{t-1},\textcolor{blue}{w_h})}{\textcolor{blue}{\partial w_h}}+ \textcolor{blue}{\sum_{i=1}^{t-1}} \left(\textcolor{green}{\prod_{j=i+1}^{t}} \frac{\partial f(x_{j},\textcolor{green}{h_{j-1}},w_h)}{\textcolor{green}{\partial h_{j-1}}} \right) \frac{\partial f(x_{i},h_{i-1},\textcolor{blue}{w_h})}{\textcolor{blue}{\partial w_h}}.$$
在上面的式子里面, $b_t$ 可以理解为 $w_h$ 对于 $t$ 时刻的隐状态 $h_t$ 的影响强度, $c_t$ 可以理解为上一时刻隐状态 $h_{t-1}$ 对于当前 $h_t$ 的影响强度.
# RNN缓解梯度问题的一些策略
Reveiw:
可以看到在上一节的结论里, 绿色的部分和蓝色的部分都会导致梯度问题. 因而我们很少直接利用上式计算RNN的梯度.
# Truncating Time Steps
- 为了避免梯度爆炸, 我们可以只计算从当前时间步往前 $\tau$ 个时间步的一小部分. 这会使梯度的传导距离变短, 让我们只关注当前时间步附近的一段序列. 实践表明这种方法还有一定 正则化 的作用在里面, 它倾向于让模型变得更简单稳定.
- 通常我们可以在一定时间步后detach掉一些部分, 就像 下面这段代码里面一样:
| |
# Randomized Truncation
我们可以人为地设定 $\tau$, 自然也可以让 $\tau$ 随机变化梯度传播距离.
定义随机变量 $\xi_t$ , 有 $P(\xi_t = 0) = 1-\pi_t$ 和 $P(\xi_t = \pi_t^{-1}) = \pi_t$, 其中 $\pi_t$ 是人为设定的参数且 $0 \leq \pi_t \leq 1$. 上面的规定是为了保证 $E[\xi_t] = 1$, 进一步保证数值稳定性2
- 从而有: $$z_t= \frac{\partial f(x_{t},h_{t-1},w_h)}{\partial w_h} +\xi_t \frac{\partial f(x_{t},h_{t-1},w_h)}{\partial h_{t-1}} \frac{\partial h_{t-1}}{\partial w_h}$$
- 在$\xi_t=0$时梯度停止传播
在实际过程中, 随机化截断的效果并没有定长截断的效果好.3
# 截断方式可视化
不同的截断方式代表了梯度不同的传播距离, 上面的图表示了每一个位置的隐状态可能的影响范围.
# RNN梯度传播的细节问题
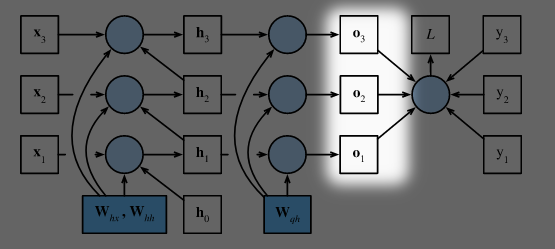
- 下面我们把 $h_t=f(x_t, h_{t-1}, w_h)$ 和 $o_t= g(h_t, w_o)$ 展开, 讨论RNN梯度传播的实际情况.
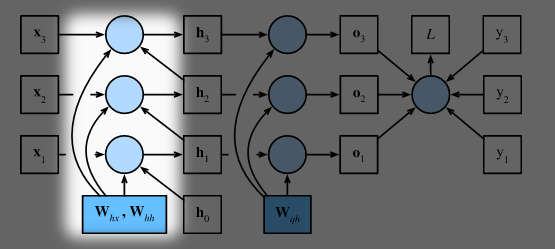
- 将 $f,g$ 展开后得到(我们先忽略激活函数和偏置): $$\begin{aligned}\mathbf{h}t &= \mathbf{W}{hx} \mathbf{x}t + \mathbf{W}{hh} \mathbf{h}{t-1},\\mathbf{o}t &= \mathbf{W}{qh} \mathbf{h}{t},\end{aligned}$$
- 根据上式可以画出三个时间步内的计算图:
其中圆圈代表运算, 方框代表变量或参数
- 在反向传播时, 我们需要计算损失函数关于参数 $\mathbf{W}{hx}$, $\mathbf{W}{hh}$, 和 $\mathbf{W}{qh}$ 的导数, 即: $\partial L/\partial \mathbf{W}{hx}$, $\partial L/\partial \mathbf{W}{hh}$, 和 $\partial L/\partial \mathbf{W}{qh}$. 计算图里面逆箭头指向参数的路径也就是反向传播的路径.
- 为了简化细节, 我们使用 $\text{prod}$ 运算符来代表任意张量,向量或者标量之间的"乘"运算.4
# Step 1: $\frac{\partial L}{\partial \mathbf{o}_t}$
$$L = \frac{1}{T} \sum_{t=1}^T l(\mathbf{o}_t, y_t).$$
 $$\frac{\partial L}{\partial \mathbf{o}_t} =\frac{1}{T}\frac{\partial l (\mathbf{o}_t, y_t)}{\partial \mathbf{o}_t} \in \mathbb{R}^q$$
$$\frac{\partial L}{\partial \mathbf{o}_t} =\frac{1}{T}\frac{\partial l (\mathbf{o}_t, y_t)}{\partial \mathbf{o}_t} \in \mathbb{R}^q$$
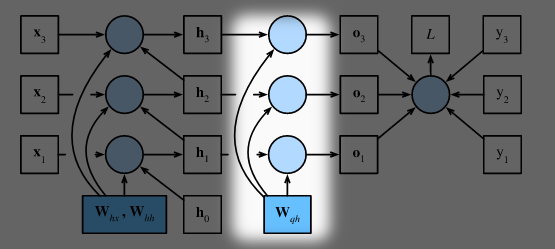
# Step 2: $\frac{\partial L}{\partial \mathbf{W}_{qh}}$
根据计算图, 损失函数对 $\mathbf{W}_{qh}$ 的梯度依赖于 $\mathbf{o}1, \ldots, \mathbf{o}T$, 利用链式法则有:
$$\frac{\partial L}{\partial \mathbf{W}{qh}}
= \sum{t=1}^T \text{prod}\left(\frac{\partial L}{\partial \mathbf{o}t}, \frac{\partial \mathbf{o}t}{\partial \mathbf{W}{qh}}\right)
= \sum{t=1}^T \frac{\partial L}{\partial \mathbf{o}_t} \mathbf{h}_t^\top$$
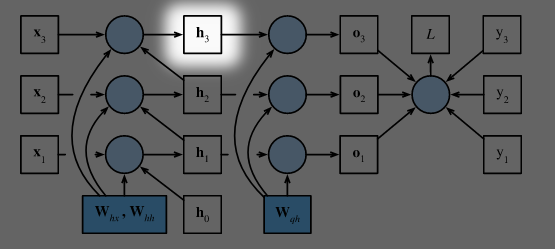
# Step 3: $\frac{\partial L}{\partial \mathbf{h}_t}$
我们先来看看对于最后一个时间步 $T$ 来说, 梯度 $\frac{\partial L}{\partial \mathbf{h}T}$ 的计算:
$$\frac{\partial L}{\partial \mathbf{h}T} = \text{prod}\left(\frac{\partial L}{\partial \mathbf{o}T}, \frac{\partial \mathbf{o}T}{\partial \mathbf{h}T} \right) = \mathbf{W}{qh}^\top \frac{\partial L}{\partial \mathbf{o}T}$$
 在 $t<T$ 的时候计算变得复杂起来, 因为 $h_t$ 的梯度同时依赖于 $o_t$ 和 $h{t+1}$
在 $t<T$ 的时候计算变得复杂起来, 因为 $h_t$ 的梯度同时依赖于 $o_t$ 和 $h{t+1}$
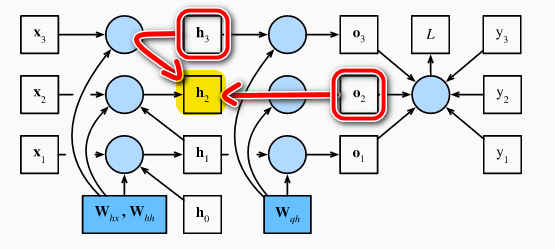 根据链式法则有:
$$\frac{\partial L}{\partial \mathbf{h}t} = \text{prod}\left(\frac{\partial L}{\partial \mathbf{h}{t+1}}, \frac{\partial \mathbf{h}{t+1}}{\partial \mathbf{h}t} \right) + \text{prod}\left(\frac{\partial L}{\partial \mathbf{o}t}, \frac{\partial \mathbf{o}t}{\partial \mathbf{h}t} \right) = \mathbf{W}{hh}^\top \frac{\partial L}{\partial \mathbf{h}{t+1}} + \mathbf{W}{qh}^\top \frac{\partial L}{\partial \mathbf{o}t}$$
转化为通项公式:
$$\frac{\partial L}{\partial \mathbf{h}t}= \sum{i=t}^T {\left(\mathbf{W}{hh}^\top\right)}^{T-i} \mathbf{W}{qh}^\top \frac{\partial L}{\partial \mathbf{o}{T+t-i}}.$$
即使我们省略了激活函数, 从中我们已经能够看到一些问题: 表达式里面 $\mathbf{W}{hh}^\top$ 的指数部分可能会很大, 在 $\mathbf{W}{hh}^\top$ 里面特征值大于 $1$ 的部分会梯度爆炸, 而特征值小于 $1$ 的部分会梯度消失.
在多次矩阵连乘以后, 一个向量会越来越靠近特征值最大的特征向量的方向.
根据链式法则有:
$$\frac{\partial L}{\partial \mathbf{h}t} = \text{prod}\left(\frac{\partial L}{\partial \mathbf{h}{t+1}}, \frac{\partial \mathbf{h}{t+1}}{\partial \mathbf{h}t} \right) + \text{prod}\left(\frac{\partial L}{\partial \mathbf{o}t}, \frac{\partial \mathbf{o}t}{\partial \mathbf{h}t} \right) = \mathbf{W}{hh}^\top \frac{\partial L}{\partial \mathbf{h}{t+1}} + \mathbf{W}{qh}^\top \frac{\partial L}{\partial \mathbf{o}t}$$
转化为通项公式:
$$\frac{\partial L}{\partial \mathbf{h}t}= \sum{i=t}^T {\left(\mathbf{W}{hh}^\top\right)}^{T-i} \mathbf{W}{qh}^\top \frac{\partial L}{\partial \mathbf{o}{T+t-i}}.$$
即使我们省略了激活函数, 从中我们已经能够看到一些问题: 表达式里面 $\mathbf{W}{hh}^\top$ 的指数部分可能会很大, 在 $\mathbf{W}{hh}^\top$ 里面特征值大于 $1$ 的部分会梯度爆炸, 而特征值小于 $1$ 的部分会梯度消失.
在多次矩阵连乘以后, 一个向量会越来越靠近特征值最大的特征向量的方向.
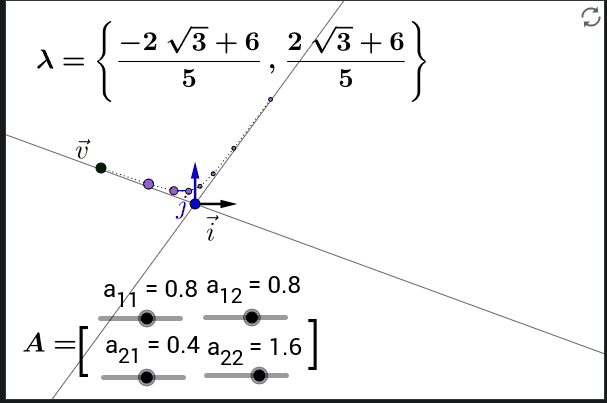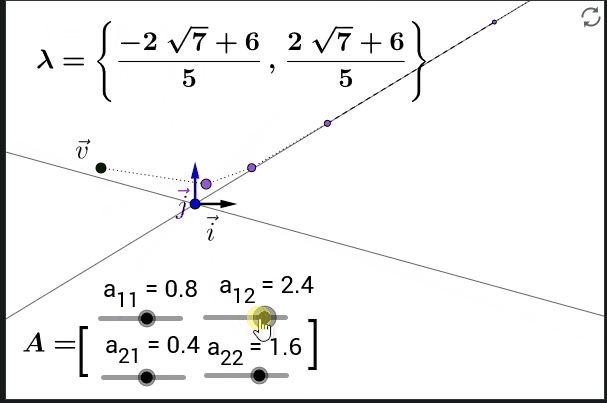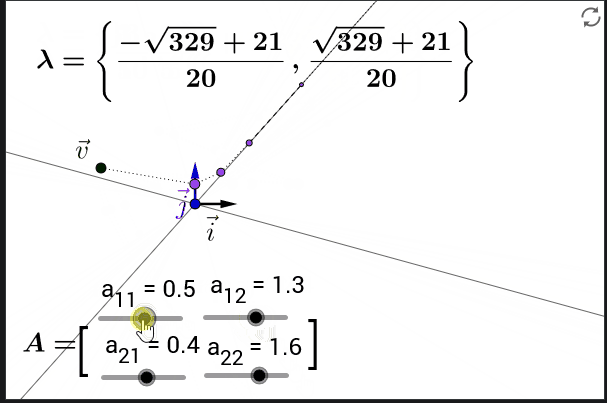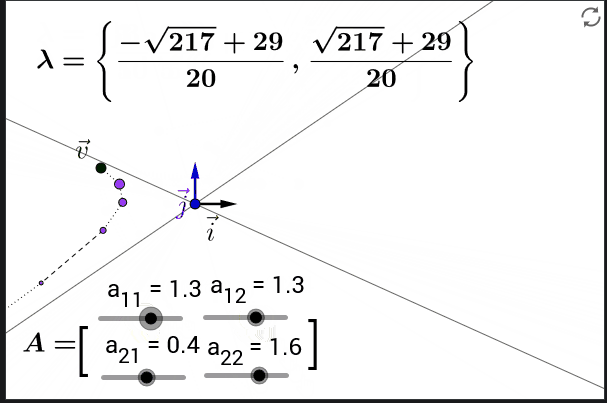 5
5
# Step 4: $\partial L / \partial \mathbf{W}{hx}$ and $\partial L / \partial \mathbf{W}{hh}$,
最后我们基于$\frac{\partial L}{\partial \mathbf{h}t}$计算隐藏层参数的梯度: $\partial L / \partial \mathbf{W}{hx} \in \mathbb{R}^{h \times d}$ 和 $\partial L / \partial \mathbf{W}{hh} \in \mathbb{R}^{h \times h}$, $$ \begin{aligned} \frac{\partial L}{\partial \mathbf{W}{hx}} &= \sum_{t=1}^T \text{prod}\left(\frac{\partial L}{\partial \mathbf{h}t}, \frac{\partial \mathbf{h}t}{\partial \mathbf{W}{hx}}\right) = \sum{t=1}^T \frac{\partial L}{\partial \mathbf{h}t} \mathbf{x}t^\top,\\ \frac{\partial L}{\partial \mathbf{W}{hh}} &= \sum{t=1}^T \text{prod}\left(\frac{\partial L}{\partial \mathbf{h}t}, \frac{\partial \mathbf{h}t}{\partial \mathbf{W}{hh}}\right) = \sum{t=1}^T \frac{\partial L}{\partial \mathbf{h}t} \mathbf{h}{t-1}^\top, \end{aligned} $$
- 其中公共的部分 $\frac{\partial L}{\partial \mathbf{h}_t}$ 可以存储起来, 避免重复计算.
- 影响梯度稳定性的部分主要是Step3里面的 $\frac{\partial L}{\partial \mathbf{h}_t}$