D2L-58-深度循环神经网络

Last updated Apr 18, 2022 Edit Source

• All
• Rnn
• Deep learning

Tags: #RNN #DeepLearning

• 和MLP与CNN中一样, 我们可以通过添加更多的层来增强网络的表达能力. 但不同的是, 增加的每一层都需要在时间步上展开, 就像上图一样.
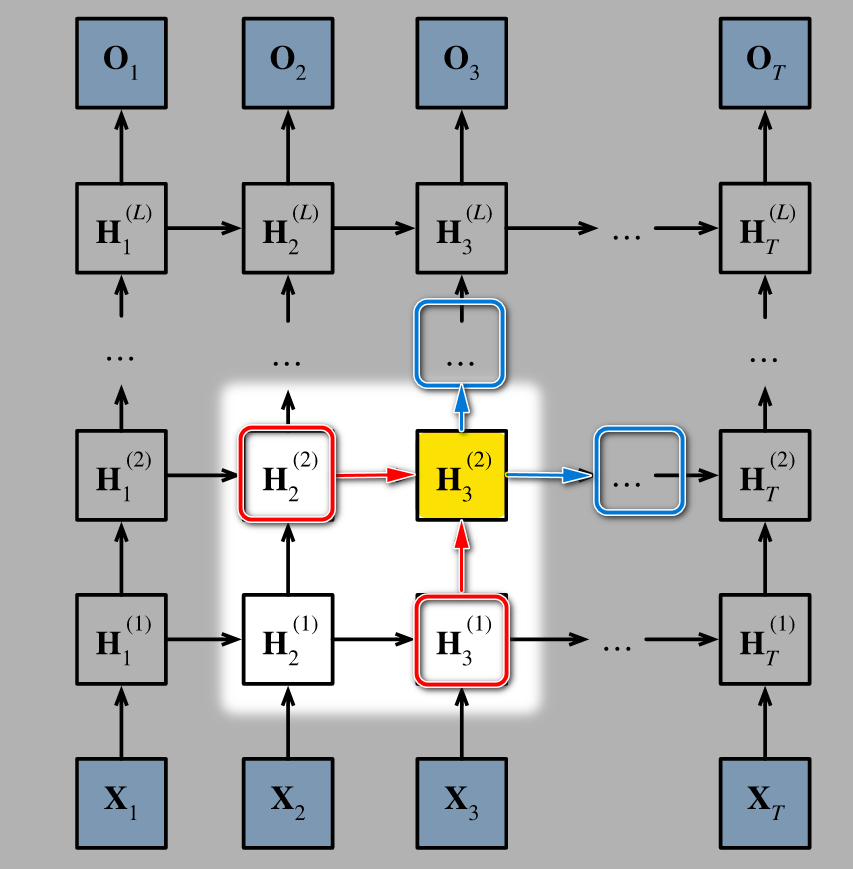
• 具体的来说, 除了边缘部分外, 每一个隐状态 $H^{(l)}_t$ 同时接受上一层同一时间步的 $\textcolor{red}{H^{(l-1)}t}$ 和同一层上一时间步的 $\textcolor{red}{H^{(l)}{t-1}}$ 作为输入, 并且输出到下一层同一时间步的 $\textcolor{royalblue}{H^{(l+1)}t}$ 和同一层下一时间步的 $\textcolor{royalblue}{H^{(l)}{t+1}}$
• 用GRU或LSTM的隐状态代替上图中的隐状态，便得到深度GRU或深度LSTM。

• 假设在时间步 $t$ 有一个小批量的输入数据 $\mathbf{X}_t \in \mathbb{R}^{n \times d}$（样本数：$n$，每个样本中的输入数：$d$）。

• 同时，将 $l^\mathrm{th}$ 隐藏层（$l=1,\ldots,L$）的隐状态设为 $\mathbf{H}_t^{(l)} \in \mathbb{R}^{n \times h}$（隐藏单元数：$h$），输出层变量设为 $\mathbf{O}_t \in \mathbb{R}^{n \times q}$（输出数：$q$）。

• 设置 $\mathbf{H}_t^{(0)} = \mathbf{X}t$，第 $l$ 个隐藏层使用激活函数 $\phi_l$，则： $$\mathbf{H}t^{(l)} = \phi_l(\mathbf{H}t^{(l-1)} \mathbf{W}{xh}^{(l)} + \mathbf{H}{t-1}^{(l)} \mathbf{W}{hh}^{(l)} + \mathbf{b}_h^{(l)})$$

  • 其中，权重 $\mathbf{W}{xh}^{(l)} \in \mathbb{R}^{h \times h}$，$\mathbf{W}{hh}^{(l)} \in \mathbb{R}^{h \times h}$ 和偏置 $\mathbf{b}_h^{(l)} \in \mathbb{R}^{1 \times h}$ 都是第 $l$ 个隐藏层的参数。

• 输出层的计算仅基于最终第 $l$ 个隐藏层的隐状态： $$\mathbf{O}_t = \mathbf{H}t^{(L)} \mathbf{W}{hq} + \mathbf{b}_q$$

在框架里面可以很容易的实现多层RNN, 比如多层LSTM在 PyTorch 里面可以定义为:

1

nn.LSTM(num_inputs, num_hiddens, num_layers)