D2L-63-Beam Search
# 束搜索
Tags: #BeamSearch #DynamicProgramming
- 在 Seq2Seq里面预测的时候, 我们直接就将上一步预测概率最大的选项输入到下一个时间步, 其实这是一种贪心策略: 最大化当前时间步的预测概率. 而贪心算法常常不能找到全局的最优解, 我们能怎样改进呢?
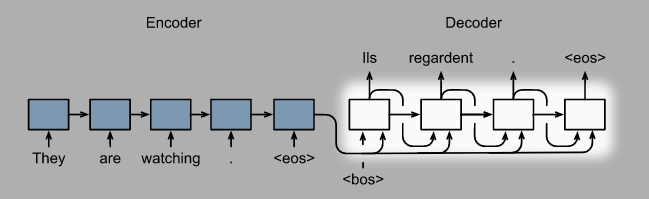
# 贪心 Greedy Search
我们先来评估一下贪心算法的时间复杂度, 我们需要计算 $T$ 个时间步的 $|\mathcal{Y}|$ 个概率, 总的时间复杂度为: $$\mathcal{O}({T}\cdot\left|\mathcal{Y}\right|)$$
# 穷举算法 Exhaustive Search
如果搜索空间不大, 我们可以直接穷举所有可能的序列 $y_1, \cdots, y_{t-1}, y_{t}$, 这时的时间复杂度为:$$\mathcal{O}(\left|\mathcal{Y}\right|^{T})$$
其中$|\mathcal{Y}|$ 表示输出词表的大小(包括<eos>), 由于词表或者时间步常常较大, 所以穷举在计算复杂度上是不可行的
# Viterbi
求解最优序列也是HMM模型里面的一个问题, 而最常用的算法就是 Viterbi Algorithm了. 在这个问题里面, Viterbi的复杂度为:$$\mathcal{O}({T}\cdot\left|\mathcal{Y}\right|^2)$$ 比穷举的指数复杂度好多了, 但是$|\mathcal{Y}|^2$依然是一个很大的项, 我们希望开销更小一点.
# Beam Search
束搜索就是开销介于Viterbi和贪心之间的那个算法了: 通过选定一个 束宽(beam size)$k$, 我们在每一个时间步只选择概率最高的 $k$ 条路径, 进一步减少了计算开销:
$$\mathcal{O}(k\cdot{T}\cdot\left|\mathcal{Y}\right|)$$
在时间步$1$,我们选择具有最高条件概率的$k$个词元。这$k$个词元将分别是$k$个候选输出序列的第一个词元。在随后的每个时间步,基于上一时间步的$k$个候选输出序列,我们将继续从$k\left|\mathcal{Y}\right|$个可能的选择中挑出具有最高条件概率的$k$个候选输出序列。
# 平衡序列长度
- 束搜索在最后找出的$k$个序列长度可能是不等的, 而长序列的概率本来就较低. 为了公平的选出最优序列, 我们对序列概率进行了加权: $$ \frac{1}{L^\alpha} \log P(y_1, \ldots, y_{L}\mid \mathbf{c}) = \frac{1}{L^\alpha} \sum_{t’=1}^L \log P(y_{t’} \mid y_1, \ldots, y_{t’-1}, \mathbf{c})$$
- 其中$L$是最终候选序列的长度,$\alpha$通常设置为$0.75$。
- 这种"平衡序列长度对结果影响"的思路和 BLEU很相似
# 总结
- 贪心算法是记忆力为 $1$ 的小傻瓜
- 而Viterbi的记忆力为每一个时间步的所有选项大小(vocab_size: $|\mathcal{Y}|$ ), 所以能够找到最优的序列.
- Beam Search是介于两者之间的, 不一定能够找到最优的方法, 但是没有贪心那么傻.
- 后面两者都是动态规划算法.
- 实际上,贪心搜索可以看作是一种束宽为 $1$ 的特殊的束搜索, Viterbi是束宽为 $|\mathcal{Y}|$ 的束搜索。 通过灵活地选择束宽,束搜索可以在正确率和计算代价之间进行权衡。