D2L-64-Kernel Regression
# Nadaraya-Watson Kernel Regression
Tags: #KernelRegression #Nonparametric #Attention #MachineLearning
# Intuition
# Definition
$$f(x) = \sum_{i=1}^n \frac{K(x - x_i)}{\sum_{j=1}^n K(x - x_j)} y_i$$
其中是$K$ 是 核(kernel), 上面的估计器(Estimator)也被称为 Nadaraya-Watson核回归(Nadaraya-Watson kernel regression)
在核为高斯核 (Gaussian Kernel) 的时候: $$K(u) = \frac{1}{\sqrt{2\pi}} \exp(-\frac{u^2}{2})$$ $$\begin{split}\begin{aligned} f(x) &=\sum_{i=1}^n \frac{K(x - x_i)}{\sum_{j=1}^n K(x - x_j)} y_i\\ &= \sum_{i=1}^n \frac{\exp\left(-\frac{1}{2}(x - x_i)^2\right)}{\sum_{j=1}^n \exp\left(-\frac{1}{2}(x - x_j)^2\right)} y_i \&= \sum_{i=1}^n \mathrm{softmax}\left(-\frac{1}{2}(x - x_i)^2\right) y_i. \end{aligned}\end{split}$$ ^33f5b4
值得注意的是,Nadaraya-Watson核回归是一个非参数模型. 可以看到上式里面没有任何参数, 模型的拟合结果完全由样本点决定.
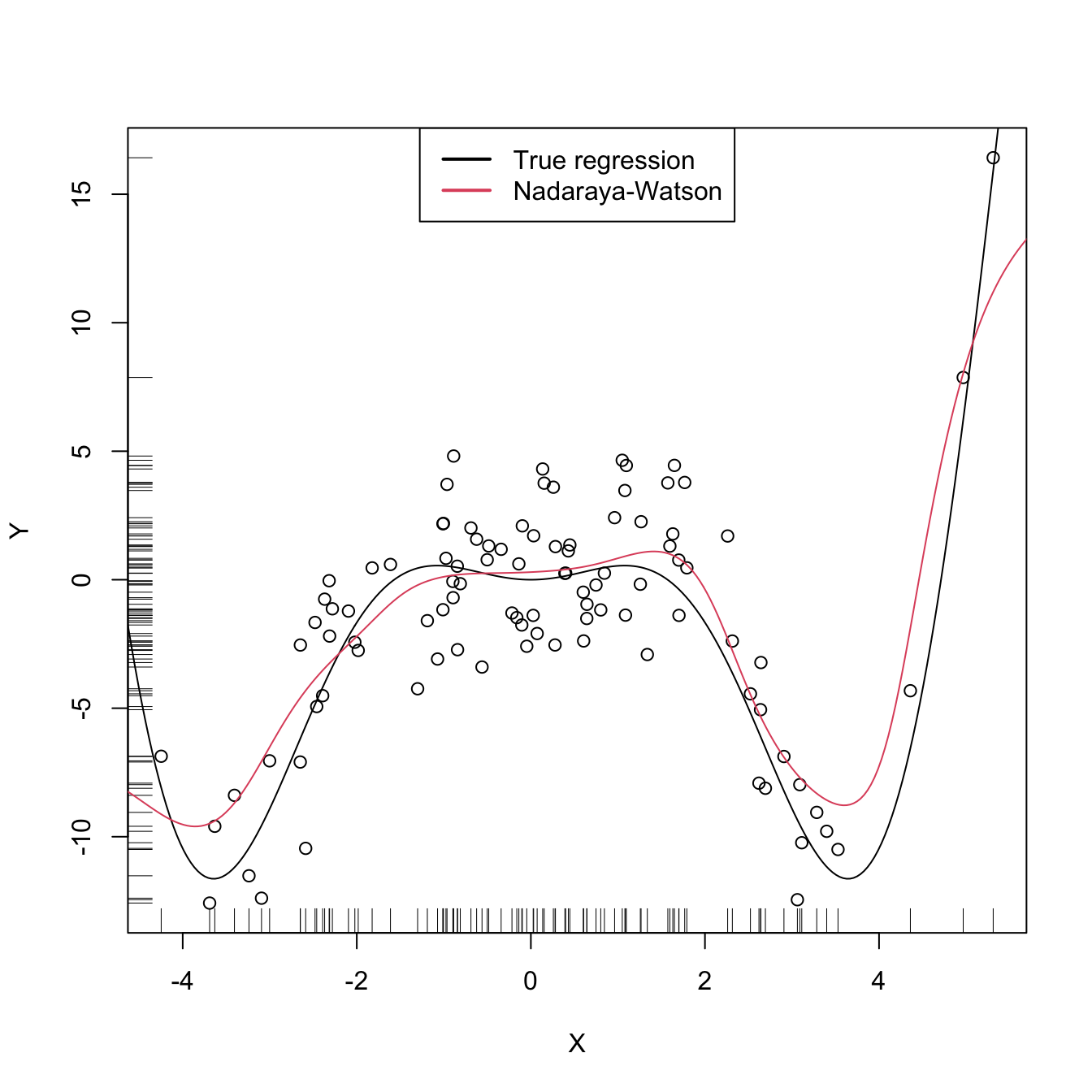
# Example of Nadaraya–Watson Estimator in practice
# Kernel Regression and Attention
D2L-66-Kernel Regression and Attention