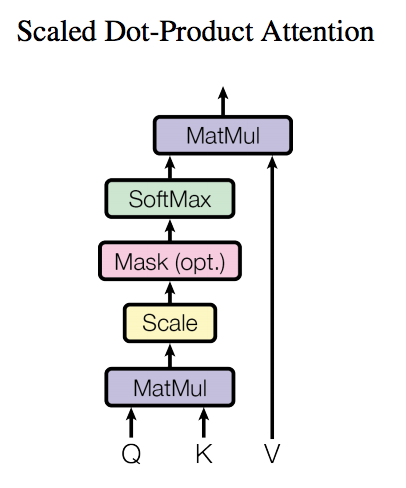
D2L-69-Scaled Dot-Product Attention

Last updated Apr 21, 2022 Edit Source

• All
• Attention
• Deep learning

Tags: #Attention #DeepLearning

¹

• 相比Additive Attention, 使用点积可以得到计算效率更高的Scoring Function. 但是点积操作要求查询和键具有相同的长度 $d$。

• 我们知道 内积可以衡量两个向量之间的相似程度, 所以我们可以这样解读缩放点积注意力:

  • 注意力机制是Values的一个加权平均, 而缩放点积注意力会赋予和 Query 更相似的 Key-Value Pair 更高的权重.

• 假设Query $\mathbf q$ 和Key $\mathbf k$ 的所有元素都是独立的随机变量，并且均值为 $0$, 方差为 $1$. 则它们的点积 $\mathbf q^\top\mathbf k$ 内元素的均值为 $0$，方差为 $d$。

  • 为确保结果的方差仍为 $1$，我们将点积除以 $\sqrt{d}$，就得到了缩放点积注意力（scaled dot-product attention）Scoring Function： $$a(\mathbf q, \mathbf k) = \frac{\mathbf{q}^\top \mathbf{k}} {\sqrt{d}}$$

• 缩放点积注意力里面是没有任何参数的, 这是它和加性注意力的一个区别.

• 在实践中，我们通常从小批量的角度来考虑提高效率

• 例如一个Batch需要基于 $n$ 个 Query 和 $m$ 个 Key-value pair 计算注意力，其中Query和Key的长度为 $d$，Value的长度为 $v$, 查询 $\mathbf Q\in\mathbb R^{n\times d}$、键 $\mathbf K\in\mathbb R^{m\times d}$ , 值 $\mathbf V\in\mathbb R^{m\times v}$ .

  • 则缩放点积注意力为： $$ \mathrm{softmax}\left(\frac{\mathbf Q \mathbf K^\top }{\sqrt{d}}\right) \mathbf V \in \mathbb{R}^{n\times v}.$$

• 代码实现:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17

class DotProductAttention(nn.Module):
    """缩放点积注意力"""
    def __init__(self, dropout, **kwargs):
        super(DotProductAttention, self).__init__(**kwargs)
        self.dropout = nn.Dropout(dropout)

    # queries的形状：(batch_size，查询的个数，d)
    # keys的形状：(batch_size，“键－值”对的个数，d)
    # values的形状：(batch_size，“键－值”对的个数，值的维度)
    # valid_lens的形状:(batch_size，)或者(batch_size，查询的个数)
    def forward(self, queries, keys, values, valid_lens=None):
        # 获取query的长度(key的长度)
        d = queries.shape[-1]
        # 设置transpose_b=True为了交换keys的最后两个维度
        scores = torch.bmm(queries, keys.transpose(1,2)) / math.sqrt(d)
        self.attention_weights = masked_softmax(scores, valid_lens)
        return torch.bmm(self.dropout(self.attention_weights), values)

• 在代码里面我们还使用了 Dropout来进行正则化