D2L-71-Multi-Head_Attention

Last updated Apr 27, 2022 Edit Source

# 多头注意力

2022-04-27

Tags: #Attention #Multi-headAttention #DeepLearning

多头注意力就是对 Query, Key, Value 进行一些线性变换, 并行地计算多个注意力, 期望模型能学习到多样化的依赖关系.

Another way of seeing it: 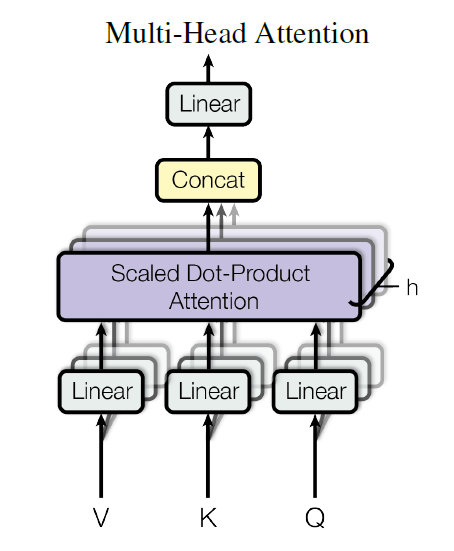¹

# 模型构建

下面我们给出 Multi-Head Attention 的形象化表示:

# Part 1

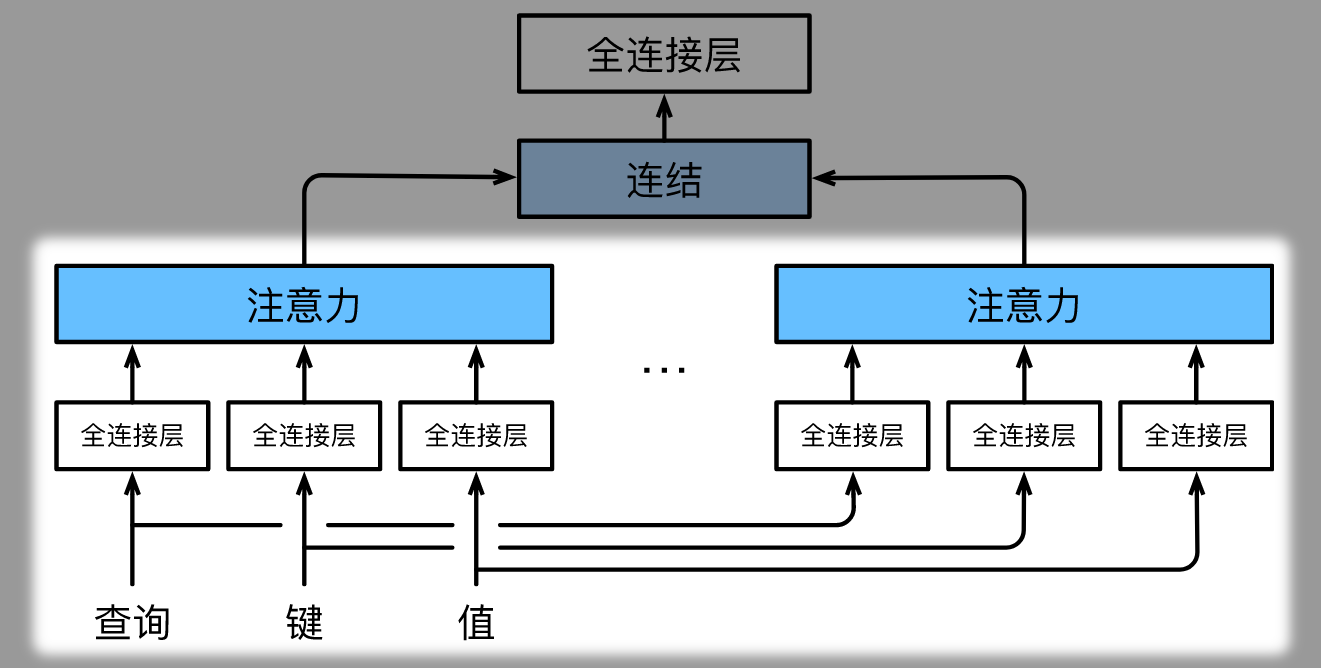
给定 Query $\mathbf{q} \in \mathbb{R}^{d_q}$、Key $\mathbf{k} \in \mathbb{R}^{d_k}$ 和 Value $\mathbf{v} \in \mathbb{R}^{d_v}$，则每个注意力头 $\mathbf{h}_i$（$i = 1, \ldots, h$）的计算方法为： $$\mathbf{h}_i = f(\mathbf W_i^{(q)}\mathbf q, \mathbf W_i^{(k)}\mathbf k,\mathbf W_i^{(v)}\mathbf v) \in \mathbb R^{p_v}$$
- 其中，可学习的参数包括
  - $\mathbf W_i^{(q)}\in\mathbb R^{p_q\times d_q}$、 $\mathbf W_i^{(k)}\in\mathbb R^{p_k\times d_k}$ 和 $\mathbf W_i^{(v)}\in\mathbb R^{p_v\times d_v}$，
  - 以及代表注意力汇聚的函数 $f$。$f$ 可以是 Attention Scoring Function 中的加性注意力或缩放点积注意力。

# Part 2

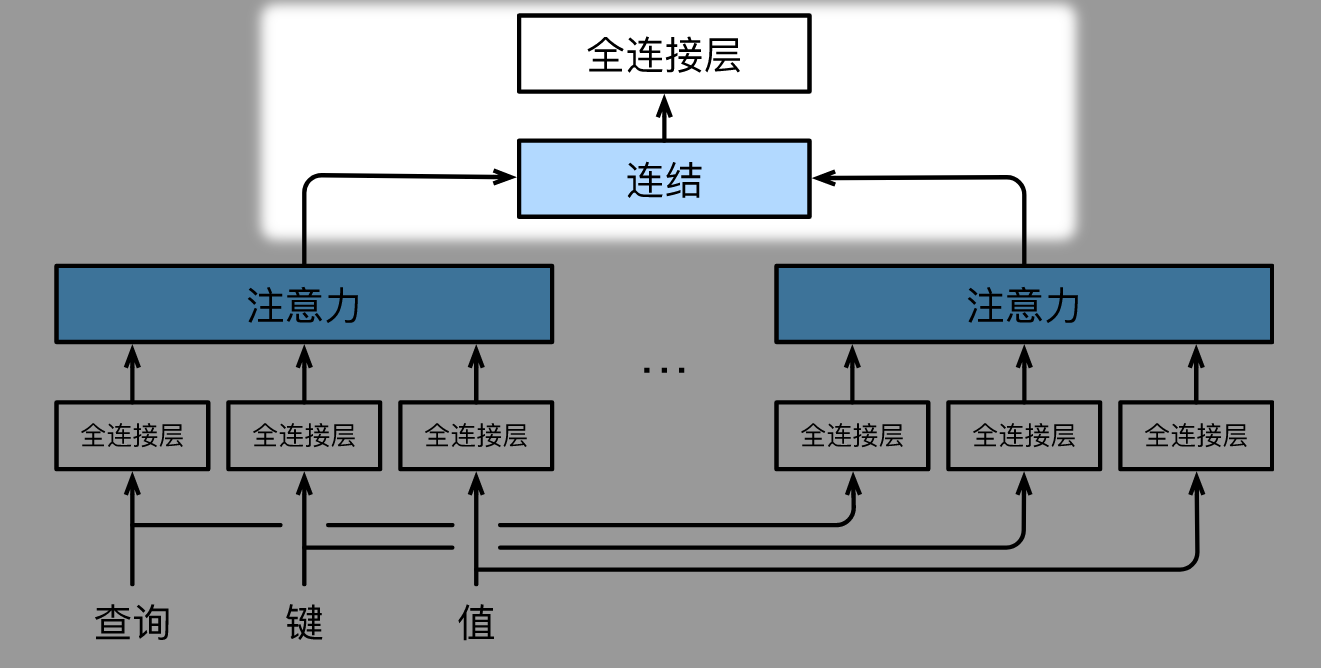
然后我们需要汇聚 $h$ 个注意力头的结果. 我们使用一个 FC 来进行汇聚 (也就是先进行 Concatenation, 再进行一个线性变换). $$\mathbf W_o \begin{bmatrix}\mathbf h_1\\vdots\\mathbf h_h\end{bmatrix} \in \mathbb{R}^{p_o}$$
- 其中可学习的参数为 $\mathbf W_o\in\mathbb R^{p_o\times h p_v}$
基于这种设计，每个头都可能会关注输入的不同部分，可以表示比简单加权平均值更复杂的函数。

# 模型实现

模型实现的关键在于: 并行地计算 $h$ 个头的注意力.

# Attention Pooling 参数规模的问题

首先, 因为多头注意力引入了大量的全连接层, 这会极大地增加 Attention Pooling 的参数大小和计算复杂度.
为了避免这个问题, 我们令 $p_q = p_k = p_v = p_o / h$, 也就是说, 现在每一个头里面的 Query, Key, Value 都只有原来的 $1/h$ 大.
因为 Value 大小变味了原来的 $1/h$, 所以 Attention 的输出长度也只有原来的 $1/h$. 而拼接以后的 $\begin{bmatrix}\mathbf h_1\\vdots\\mathbf h_h\end{bmatrix}$ 长度和原来一样.
最后的 $\mathbf W_o$ 输入输出大小一样.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
class MultiHeadAttention(nn.Module):
    """多头注意力"""
    def __init__(self, key_size, query_size, value_size, num_hiddens,
                 num_heads, dropout, bias=False, **kwargs):
        super(MultiHeadAttention, self).__init__(**kwargs)
        self.num_heads = num_heads
        self.attention = d2l.DotProductAttention(dropout)
        self.W_q = nn.Linear(query_size, num_hiddens, bias=bias)
        self.W_k = nn.Linear(key_size, num_hiddens, bias=bias)
        self.W_v = nn.Linear(value_size, num_hiddens, bias=bias)
        self.W_o = nn.Linear(num_hiddens, num_hiddens, bias=bias)

######初始化时############################
num_hiddens, num_heads = 100, 5
attention = MultiHeadAttention(
    key_size    =   num_hiddens,
    query_size  =   num_hiddens,
    value_size  =   num_hiddens,
    num_hiddens =   num_hiddens,
    num_heads   =   num_heads,
    dropout     =   0.5 )

提问: 既然 Attention 前的线性映射缩小了 Query, Key 和 Value 的长度, 那为什么上面初始化时 key_size, query_size, value_size 还是等于 num_hiddens 呢?
- 其实 $W_q, W_k, W_v$ 表示的是将 $h$ 个小全连接层拼起来, 得到的一个"大号全连接层"的参数.

# 并行化思路

为了实现并行计算, 我们先将线性映射之后的 Query, Key, Value 的按 $Batches\times heads$ 的方式拼接在一起:
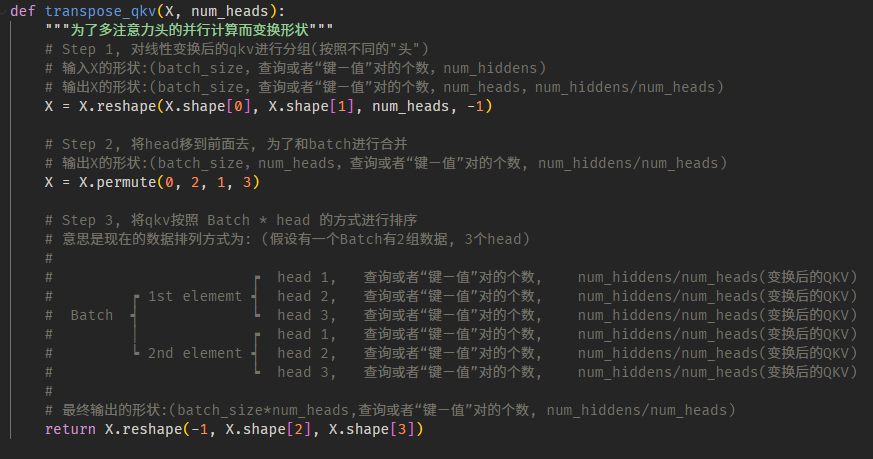
然后将拼接后的张量一起送进 Attention, 得到未融合的注意力输出,
再重新变换形状, 得到 $\begin{bmatrix}\mathbf h_1\\vdots\\mathbf h_h\end{bmatrix}$
最后再经过一个全连接层 $\mathbf W_o$, 得到融合后的注意力输出

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
def forward(self, queries, keys, values, valid_lens):
        # queries，keys，values的形状:
        # (batch_size，查询或者“键－值”对的个数，num_hiddens)
        # valid_lens　的形状:
        # (batch_size，)或(batch_size，查询的个数)
        # 经过变换后，输出的queries，keys，values　的形状:
        # (batch_size*num_heads，查询或者“键－值”对的个数，
        # num_hiddens/num_heads)
        queries = transpose_qkv(self.W_q(queries), self.num_heads)
        keys = transpose_qkv(self.W_k(keys), self.num_heads)
        values = transpose_qkv(self.W_v(values), self.num_heads)

        if valid_lens is not None:
            # 在轴0，将第一项（标量或者矢量）复制num_heads次，
            # 然后如此复制第二项，然后诸如此类。
            valid_lens = torch.repeat_interleave(
                valid_lens, repeats=self.num_heads, dim=0)

        # output的形状:(batch_size*num_heads，查询的个数，
        # num_hiddens/num_heads)
        output = self.attention(queries, keys, values, valid_lens)

        # output_concat的形状:(batch_size，查询的个数，num_hiddens)
        output_concat = transpose_output(output, self.num_heads)
        return self.W_o(output_concat)

# 并行化细节

详细地说, 张量形状的变化如下图所示:

From Attention is All You Need ↩︎

Cyan's Blog

D2L-71-Multi-Head_Attention

# 多头注意力

# 模型构建

# Part 1

# Part 2

# 模型实现

# Attention Pooling 参数规模的问题

# 并行化思路

# 并行化细节

Backlinks

Interactive Graph