凸组合 - Convex Combination
# Convex Combination
2022-04-18
Tags: #NonlinearProgreamming #Math #ConvexCombination
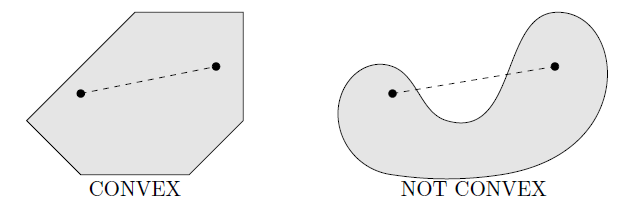
A convex combination of points $\mathbf{x}^{(1)}, \mathbf{x}^{(2)}, \ldots, \mathbf{x}^{(k)} \in \mathbb{R}^{n}$ is a “weighted average”: a linear combination $$ \lambda_{1} \mathbf{x}^{(1)}+\lambda_{2} \mathbf{x}^{(2)}+\cdots+\lambda_{k} \mathbf{x}^{(k)} $$ where $\lambda_{1}+\lambda_{2}+\cdots+\lambda_{k}=1$ and $\lambda_{1}, \ldots, \lambda_{k} \geq 0$
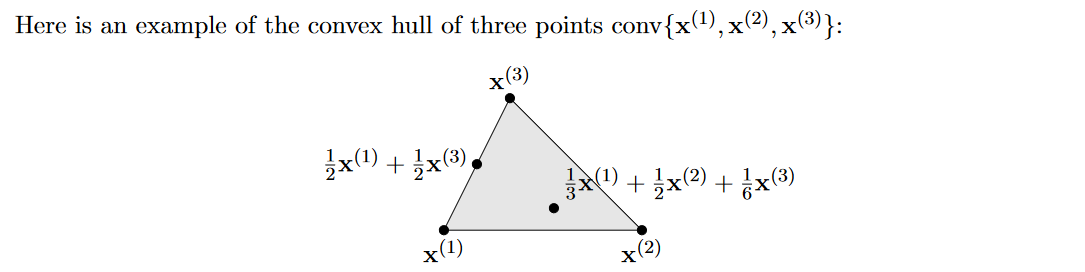
The convex hull $\operatorname{conv}(S)$ of a set of points $S$ is sometimes defined as the set of all convex combinations of points from $S$.
In the plane, you can visualize $\operatorname{conv}(S)$ as the interior of a rubber band stretched around points in $S$.
Ref: Original File(@ConvexCombination)