从二项分布到泊松分布再到指数分布-From Binomial Distribution to Poisson Distribution to Exponential Distribution
# From Binomial Distribution to Poisson Distribution to Exponential Distribution
Tags: #Math/Probability #PoissonDistribution #BinomialDistribution #ExponentialDistribution
- 这两个回答讲的挺好:
- 泊松分布的现实意义是什么,为什么现实生活多数服从于泊松分布? - 马同学的回答 - 知乎 https://www.zhihu.com/question/26441147/answer/429569625
- 指数分布公式的含义是什么? - 马同学的回答 - 知乎 https://www.zhihu.com/question/24796044/answer/673838656
# Binomial Distribution
- 对于概率为 $p$ 的事件, $n$ 次试验里面发生 $k$ 次的概率为: $$\left(\begin{array}{l} n \\ k \end{array}\right) p^{k}(1-p)^{n-k}$$
# Poisson Distribution
在 $n\rightarrow \infty$ 的时候, Binominal Distribution 等价于期望相同的 Poisson Distribution: $$\lim _{n \rightarrow \infty}\left(\begin{array}{l} n \\ k \end{array}\right) p^{k}(1-p)^{n-k}$$
二项分布的期望为: $E(X)=np$, 泊松分布的期望为: $\lambda$. 因为期望 $E(X)$ 相同: $$p=\frac{\lambda}{n}$$
带入上式, 得到: $$\lim _{n \rightarrow \infty}\left(\begin{array}{l} n \\ k \end{array}\right) p^{k}(1-p)^{n-k}=\lim _{n \rightarrow \infty}\left(\begin{array}{l} n \\ k \end{array}\right)\left(\frac{\lambda}{n}\right)^{k}\left(1-\frac{\lambda}{n}\right)^{n-k}$$
求解这个极限: $$\begin{aligned} \lim _{n \rightarrow \infty}\left(\begin{array}{l} n \\ k \end{array}\right)\left(\frac{\lambda}{n}\right)^{k}\left(1-\frac{\lambda}{n}\right)^{n-k} &=\lim _{n \rightarrow \infty} \frac{n(n-1)(n-2) \cdots(n-k+1)}{k !} \frac{\lambda^{k}}{n^{k}}\left(1-\frac{\lambda}{n}\right)^{n-k} \\ &=\lim _{n \rightarrow \infty} \frac{\lambda^{k}}{k !} \frac{n}{n} \cdot \frac{n-1}{n} \cdots \frac{n-k+1}{n}\left(1-\frac{\lambda}{n}\right)^{-k}\left(1-\frac{\lambda}{n}\right)^{n} \end{aligned}$$
其中: $$\begin{gathered} \lim _{n \rightarrow \infty} \frac{n}{n} \cdot \frac{n-1}{n} \cdots \frac{n-k+1}{n}\left(1-\frac{\lambda}{n}\right)^{-k}=1 \\ \lim _{n \rightarrow \infty}\left(1-\frac{\lambda}{n}\right)^{n}=e^{-\lambda} \end{gathered}$$
所以 $$\lim _{n \rightarrow \infty}\left(\begin{array}{l} n \\ k \end{array}\right)\left(\frac{\lambda}{n}\right)^{k}\left(1-\frac{\lambda}{n}\right)^{n-k}=\frac{\lambda^{k}\space e^{-\lambda}}{k !} $$ 也就是 Poisson Distribution 的概率密度函数
在 $n$ 很大, 也就是 $p$ 很小的时候, 两者大概相似:
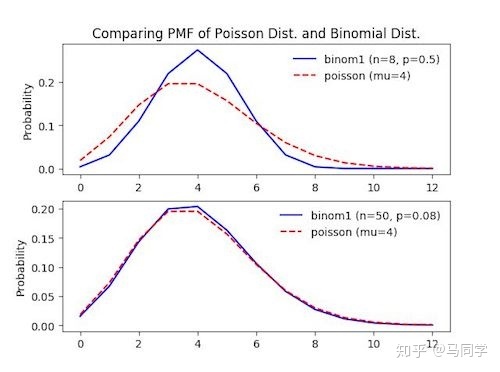
# Exponential Distribution
- The waiting times for Poisson distribution is an exponential distribution with parameter $\lambda$.
- 服从泊松分布的事件之间的时间差服从指数分布 Relationship between Poisson and exponential distribution - Cross Validated
I will use the following notation to be as consistent as possible with the wiki (in case you want to go back and forth between my answer and the wiki definitions for the poisson and exponential.)
- $N_t$: the number of arrivals during time period $t$
- $X_t$: the time it takes for one additional arrival to arrive assuming that someone arrived at time $t$
By definition, the following conditions are equivalent: $$(X_t>x)≡(N_t=N_t+x)$$
The event on the left captures the event that no one has arrived in the time interval $[t,t+x]$ which implies that our count of the number of arrivals at time $t+x$ is identical to the count at time $t$which is the event on the right.
By the complement rule, we also have: $$P(X_t≤x)=1−P(X_t>x)$$
Using the equivalence of the two events that we described above, we can re-write the above as: $$P(X_t≤x)=1−P(N_{t+x}−N_t=0)$$
But, $$P(N_{t+x}−N_t=0)=P(N_x=0)$$
Using the poisson pmf the above where $λ$ is the average number of arrivals per time unit and $x$ a quantity of time units, simplifies to: $$P(N_{t+x}−N_t=0)=\frac{(λx)^0}{0!}e^{−λx}$$
i.e. $$P(N_{t+x}−N_t=0)=e^{−λx}$$
Substituting in our original eqn, we have: $$P(X_t≤x)=1−e^{−λx}$$
The above is the cdf of a exponential pdf.